Differential equations are at the heart of many scientific and engineering disciplines. They describe how things change and can be used to solve real-world problems.
“Equations are more important to me because politics is for the present, but an equation is something for eternity.” – Albert Einstein
- Population Dynamics
The growth of a population can be described by a simple differential equation: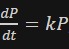
where ,P is the population, t is time, and k is a constant. This equation models exponential growth, which is common in populations without limiting factors. - Radioactive Decay
Radioactive substances decay over time. The rate of decay is proportional to the current amount of the substance, which can be modeled by the differential equation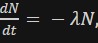
, where N is the quantity of the substance and λ is the decay constant. - Drug Concentration in the Body
The concentration of a drug in the body after administration can be modeled using differential equations. The rate of change of drug concentration depends on the dosage, the rate at which the drug is absorbed, and the rate at which it is eliminated. - Electrical Circuits
In electrical circuits, the voltage, current, and resistance are related by differential equations. For example, in an RC circuit (a circuit with resistance and capacitance), the voltage across the capacitor is described by the differential equation
, where E is the emf of the battery. - Economics
In economics, differential equations are used to model economic growth, investment strategies, and market equilibrium. For example, the Solow-Swan model of economic growth is described by a differential equation. - Physics
In physics, differential equations are used to describe motion (Newton’s second law), wave propagation, heat distribution, fluid flow, etc. For example, the motion of a pendulum is described by a second-order differential equation. - Epidemiology
In epidemiology, the spread of diseases can be modeled using differential equations. The SIR model
(susceptible, infected, recovered) is a set of differential equations that describe the dynamics of an infectious disease in a population. - Climate Science
In climate science, differential equations are used to model the Earth’s climate system, including the
atmosphere, oceans, and ice caps. These equations help scientists understand past climate changes and predict future ones. - Control Systems
In control systems, differential equations are used to describe the system’s dynamics and design controllers to achieve desired performance. For example, the control of a drone’s position and orientation involves solving differential equations. - Partial Differential Equations in Image Processing
Partial differential equations (PDEs) play a crucial role in image processing. They are used for image
enhancement, restoration, segmentation, and registration. For example, the heat equation, a type of PDE, is used for image smoothing and noise reduction.
In conclusion, differential equations are a powerful tool in mathematics and science. They provide a language to describe change and dynamics, and their solutions give us insight into the phenomena we are studying. As Isaac Newton once said, “Truth is ever to be found in simplicity, and not in the multiplicity and confusion of things.” Differential equations help us find the simple truths hidden in complex systems.