- The Problem:
Imagine the entire web as a vast network of interconnected pages. Each page is like a node in a
graph, and hyperlinks connect these nodes.
When you search for something on Google, the search engine needs to figure out which pages are
most relevant to your query. But how can it do this effectively?
- The Solution:
PageRank is an algorithm that helps rank web pages based on their importance. It was developed
by Larry Page and Sergey Brin (the founders of Google).
Instead of just counting the number of links to a page, PageRank considers the quality of those
links.
3.Intuition:
Imagine a random surfer navigating the web by clicking on links. The probability that the surfer
lands on a particular page depends on its PageRank score.
If a page is linked to by many other pages (especially important ones), it’s likely to be significant.
4.Mathematics Behind PageRank:
Damping Factor (P):
Sometimes the surfer might jump to a random page instead of following links. The damping
factor P (usually around 0.85) represents this probability.
It ensures that the surfer doesn’t get stuck in a loop and continues exploring the web.
Matrix Representation:
We represent the web graph as an adjacency matrix. Each entry in the matrix tells us
whether one page links to another.
For example, if page A links to page B, the entry A(i, j) in the matrix is 1; otherwise, it’s 0.
PageRank Vector r :
We start with a vector r where each page has an equal score.
We update r iteratively using the following formula:
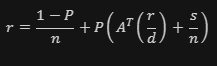
n: Total number of pages.
d: Out-degree (number of outgoing links) of the current page.
s: A vector representing the teleportation (random jump) probability
5.Example: Let’s consider a tiny web graph with three pages: A, B, and C. The adjacency matrix A looks like this:

- Calculate the out-degrees:
- d(A) = 2 (A links to B and C)
- d(B) = 1 (B links to A)
- d(C) = 2 (C links to A and B)
- Initialize r:
- r = [1, 1, 1]
- Update r iteratively until convergence:
- Apply the PageRank formula to compute new scores for A, B, and C.